encoding.nn¶

Customized NN modules in Encoding Package. For Synchronized Cross-GPU Batch Normalization, please visit encoding.nn.BatchNorm2d.

Encoding¶

class encoding.nn.Encoding(D, K)[source]¶

Encoding Layer: a learnable residual encoder.

Encoding Layer accpets 3D or 4D inputs. It considers an input featuremaps with the shape of \(C\times H\times W\) as a set of C-dimentional input features \(X=\{x_1, ...x_N\}\), where N is total number of features given by \(H\times W\), which learns an inherent codebook \(D=\{d_1,...d_K\}\) and a set of smoothing factor of visual centers \(S=\{s_1,...s_K\}\). Encoding Layer outputs the residuals with soft-assignment weights \(e_k=\sum_{i=1}^Ne_{ik}\), where

\[e_{ik} = \frac{exp(-s_k\|r_{ik}\|^2)}{\sum_{j=1}^K exp(-s_j\|r_{ij}\|^2)} r_{ik}\]

and the residuals are given by \(r_{ik} = x_i - d_k\). The output encoders are \(E=\{e_1,...e_K\}\).

Parameters

D – dimention of the features or feature channels
K – number of codeswords

Shape:

Input: \(X\in\mathcal{R}^{B\times N\times D}\) or \(\mathcal{R}^{B\times D\times H\times W}\) (where \(B\) is batch, \(N\) is total number of features or \(H\times W\).)
Output: \(E\in\mathcal{R}^{B\times K\times D}\)

Variables

codewords (Tensor) – the learnable codewords of shape (\(K\times D\))
scale (Tensor) – the learnable scale factor of visual centers

Reference:

Hang Zhang, Kristin Dana, Jianping Shi, Zhongyue Zhang, Xiaogang Wang, Ambrish Tyagi, Amit Agrawal. “Context Encoding for Semantic Segmentation. The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2018

Hang Zhang, Jia Xue, and Kristin Dana. “Deep TEN: Texture Encoding Network.” The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2017

Examples

>>> import encoding
>>> import torch
>>> import torch.nn.functional as F
>>> from torch.autograd import Variable
>>> B,C,H,W,K = 2,3,4,5,6
>>> X = Variable(torch.cuda.DoubleTensor(B,C,H,W).uniform_(-0.5,0.5), requires_grad=True)
>>> layer = encoding.Encoding(C,K).double().cuda()
>>> E = layer(X)

forward(X)[source]¶

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

DistSyncBatchNorm¶

class encoding.nn.DistSyncBatchNorm(num_features, eps=1e-05, momentum=0.1, process_group=None)[source]¶

Cross-GPU Synchronized Batch normalization (SyncBN)

Standard BN 1 implementation only normalize the data within each device (GPU). SyncBN normalizes the input within the whole mini-batch. We follow the sync-onece implmentation described in the paper 2 . Please see the design idea in the notes.

\[y = \frac{x - mean[x]}{ \sqrt{Var[x] + \epsilon}} * gamma + beta\]

The mean and standard-deviation are calculated per-channel over the mini-batches and gamma and beta are learnable parameter vectors of size C (where C is the input size).

During training, this layer keeps a running estimate of its computed mean and variance. The running sum is kept with a default momentum of 0.1.

During evaluation, this running mean/variance is used for normalization.

Because the BatchNorm is done over the C dimension, computing statistics on (N, H, W) slices, it’s common terminology to call this Spatial BatchNorm

Parameters

num_features – num_features from an expected input of size batch_size x num_features x height x width
eps – a value added to the denominator for numerical stability. Default: 1e-5
momentum – the value used for the running_mean and running_var computation. Default: 0.1
sync – a boolean value that when set to True, synchronize across different gpus. Default: True
activation – str Name of the activation functions, one of: leaky_relu or none.
slope – float Negative slope for the leaky_relu activation.

Shape:

Input: \((N, C, H, W)\)
Output: \((N, C, H, W)\) (same shape as input)

Reference:

1(1,2): Ioffe, Sergey, and Christian Szegedy. “Batch normalization: Accelerating deep network training by reducing internal covariate shift.” ICML 2015
2(1,2): Hang Zhang, Kristin Dana, Jianping Shi, Zhongyue Zhang, Xiaogang Wang, Ambrish Tyagi, and Amit Agrawal. “Context Encoding for Semantic Segmentation.” CVPR 2018

Examples

>>> m = DistSyncBatchNorm(100)
>>> net = torch.nn.parallel.DistributedDataParallel(m)
>>> output = net(input)

forward(x)[source]¶

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

SyncBatchNorm¶

class encoding.nn.SyncBatchNorm(num_features, eps=1e-05, momentum=0.1, sync=True, activation='none', slope=0.01, inplace=True)[source]¶

Cross-GPU Synchronized Batch normalization (SyncBN)

Standard BN 1 implementation only normalize the data within each device (GPU). SyncBN normalizes the input within the whole mini-batch. We follow the sync-onece implmentation described in the paper 2 . Please see the design idea in the notes.

\[y = \frac{x - mean[x]}{ \sqrt{Var[x] + \epsilon}} * gamma + beta\]

The mean and standard-deviation are calculated per-channel over the mini-batches and gamma and beta are learnable parameter vectors of size C (where C is the input size).

During training, this layer keeps a running estimate of its computed mean and variance. The running sum is kept with a default momentum of 0.1.

During evaluation, this running mean/variance is used for normalization.

Because the BatchNorm is done over the C dimension, computing statistics on (N, H, W) slices, it’s common terminology to call this Spatial BatchNorm

Parameters

num_features – num_features from an expected input of size batch_size x num_features x height x width
eps – a value added to the denominator for numerical stability. Default: 1e-5
momentum – the value used for the running_mean and running_var computation. Default: 0.1
sync – a boolean value that when set to True, synchronize across different gpus. Default: True
activation – str Name of the activation functions, one of: leaky_relu or none.
slope – float Negative slope for the leaky_relu activation.

Shape:

Input: \((N, C, H, W)\)
Output: \((N, C, H, W)\) (same shape as input)

Examples

>>> m = SyncBatchNorm(100)
>>> net = torch.nn.DataParallel(m)
>>> output = net(input)
>>> # for Inpace ABN
>>> ABN = partial(SyncBatchNorm, activation='leaky_relu', slope=0.01, sync=True, inplace=True)

extra_repr()[source]¶

Set the extra representation of the module

To print customized extra information, you should re-implement this method in your own modules. Both single-line and multi-line strings are acceptable.

forward(x)[source]¶

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

BatchNorm1d¶

class encoding.nn.BatchNorm1d(*args, **kwargs)[source]¶: Warning

BatchNorm1d is deprecated in favor of encoding.nn.SyncBatchNorm.

BatchNorm2d¶

class encoding.nn.BatchNorm2d(*args, **kwargs)[source]¶: Warning

BatchNorm2d is deprecated in favor of encoding.nn.SyncBatchNorm.

BatchNorm3d¶

class encoding.nn.BatchNorm3d(*args, **kwargs)[source]¶: Warning

BatchNorm3d is deprecated in favor of encoding.nn.SyncBatchNorm.

Inspiration¶

class encoding.nn.Inspiration(C, B=1)[source]¶

Inspiration Layer (CoMatch Layer) enables the multi-style transfer in feed-forward network, which learns to match the target feature statistics during the training. This module is differentialble and can be inserted in standard feed-forward network to be learned directly from the loss function without additional supervision.

\[Y = \phi^{-1}[\phi(\mathcal{F}^T)W\mathcal{G}]\]

Please see the example of MSG-Net training multi-style generative network for real-time transfer.

Reference:: Hang Zhang and Kristin Dana. “Multi-style Generative Network for Real-time Transfer.” arXiv preprint arXiv:1703.06953 (2017)

forward(X)[source]¶

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

UpsampleConv2d¶

class encoding.nn.UpsampleConv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, scale_factor=1, bias=True)[source]¶

To avoid the checkerboard artifacts of standard Fractionally-strided Convolution, we adapt an integer stride convolution but producing a \(2\times 2\) outputs for each convolutional window.

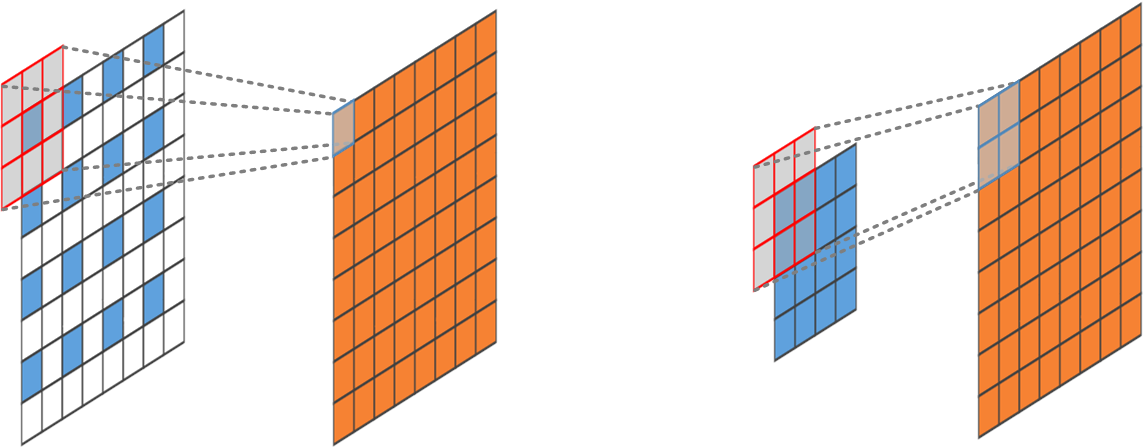
Reference:: Hang Zhang and Kristin Dana. “Multi-style Generative Network for Real-time Transfer.” arXiv preprint arXiv:1703.06953 (2017)

Parameters

in_channels (int) – Number of channels in the input image
out_channels (int) – Number of channels produced by the convolution
kernel_size (int or tuple) – Size of the convolving kernel
stride (int or tuple, optional) – Stride of the convolution. Default: 1
padding (int or tuple, optional) – Zero-padding added to both sides of the input. Default: 0
output_padding (int or tuple, optional) – Zero-padding added to one side of the output. Default: 0
groups (int, optional) – Number of blocked connections from input channels to output channels. Default: 1
bias (bool, optional) – If True, adds a learnable bias to the output. Default: True
dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1
scale_factor (int) – scaling factor for upsampling convolution. Default: 1

Shape:

Input: \((N, C_{in}, H_{in}, W_{in})\)
Output: \((N, C_{out}, H_{out}, W_{out})\) where \(H_{out} = scale * (H_{in} - 1) * stride[0] - 2 * padding[0] + kernel\_size[0] + output\_padding[0]\) \(W_{out} = scale * (W_{in} - 1) * stride[1] - 2 * padding[1] + kernel\_size[1] + output\_padding[1]\)

Variables

weight (Tensor) – the learnable weights of the module of shape (in_channels, scale * scale * out_channels, kernel_size[0], kernel_size[1])
bias (Tensor) – the learnable bias of the module of shape (scale * scale * out_channels)

Examples

>>> # With square kernels and equal stride
>>> m = nn.UpsampleCov2d(16, 33, 3, stride=2)
>>> # non-square kernels and unequal stride and with padding
>>> m = nn.UpsampleCov2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2))
>>> input = autograd.Variable(torch.randn(20, 16, 50, 100))
>>> output = m(input)
>>> # exact output size can be also specified as an argument
>>> input = autograd.Variable(torch.randn(1, 16, 12, 12))
>>> downsample = nn.Conv2d(16, 16, 3, stride=2, padding=1)
>>> upsample = nn.UpsampleCov2d(16, 16, 3, stride=2, padding=1)
>>> h = downsample(input)
>>> h.size()
torch.Size([1, 16, 6, 6])
>>> output = upsample(h, output_size=input.size())
>>> output.size()
torch.Size([1, 16, 12, 12])

forward(input)[source]¶

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

GramMatrix¶

class encoding.nn.GramMatrix[source]¶

Gram Matrix for a 4D convolutional featuremaps as a mini-batch

\[\mathcal{G} = \sum_{h=1}^{H_i}\sum_{w=1}^{W_i} \mathcal{F}_{h,w}\mathcal{F}_{h,w}^T\]

forward(y)[source]¶

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.