Implementing Synchronized Multi-GPU Batch Normalization, Do It Exactly Right

[MXNet Gluon Implementation] [PyTorch implementation]

Language: 中文

Why synchronize the BN layer?

In deep learning frameworks (Caffe, Torch. Tensorflow, PyTorch and etc.) , the implementation of Batch Normalization is only normalize the data within every single GPU due to the Data Parallelism. We implement synchronize BN for some specific tasks such as semantic segmentation, object detection because they are usually memory consuming and the mini-batch size within a single GPU is too small for BN. Therefore, we discuss the synchronized implementation here.

What is Batch Normalization (BN) and how it works?

Batch Normalization was introduced in the paper Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift , which dramatically speed up the training process of the network (enables larger learning rate) and makes the network less sensitive to the weight initialization. The idea is performing the normalization within the mini-batch. The training mode:

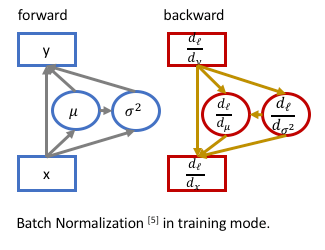
• Forward Pass: For the input data \(X={x_1, ...x_N}\), the data are normalized to be zero-mean and unit-variance, then scale and shit:

\[y_i = \gamma\cdot\frac{x_i-\mu}{\sigma} + \beta ,\]

where \(\mu=\frac{\sum_i^N x_i}{N} , \sigma = \sqrt{\frac{\sum_i^N (x_i-\mu)^2}{N}+\epsilon}\) and \(\gamma, \beta\) are the learnable scale and shift parameters.

• Backward Pass:

We need to consider the partial gradients from output \(\frac{d_\ell}{d_{y_i}}\), and the gradients from \(\frac{d_\ell}{d_\mu}\) and \(\frac{d_\ell}{d_\sigma}\), because the mean and variance are the function of the input: (We use the notations of partial gradients here.)

\[\frac{d_\ell}{d_{x_i}} = \frac{d_\ell}{d_{y_i}}\cdot\frac{\partial_{y_i}}{\partial_{x_i}} + \frac{d_\ell}{d_\mu}\cdot\frac{d_\mu}{d_{x_i}} + \frac{d_\ell}{d_\sigma}\cdot\frac{d_\sigma}{d_{x_i}},\]

where \(\frac{\partial_{y_i}}{\partial_{x_i}}=\frac{\gamma}{\sigma}, \frac{d_\ell}{d_\mu}=-\frac{\gamma}{\sigma}\sum_i^N\frac{d_\ell}{d_{y_i}}, \frac{d_\mu}{d_{x_i}}=\frac{1}{N} \text{ and } \frac{d_\sigma}{d_{x_i}}=-\frac{1}{\sigma}(\frac{x_i-\mu}{N})\).

• Data Parallel in Deep Learning Frameworks:

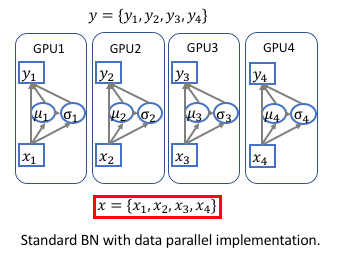
Standard DataParallel pipeline of public frameworks (MXNet, PyTorch…) in each training iters:

• duplicate the network (weights) to all the GPUs,
• split the training batch to each GPU,
• forward and backward to calculate gradient,
• update network parameters (weights) then go to next iter.

Therefore, the standard Batch Normalization only normalize the data within each GPU individually.

Synchronized Batch Normalization implementation

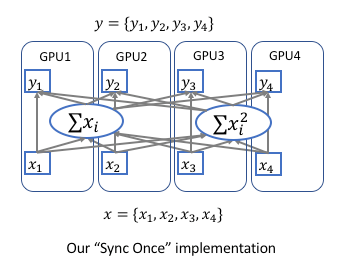
• Forforward Pass:

  The mean \(\mu\) and variance \(\sigma\) need to be calculated across all the GPUs. Instead of synchronizing twice for calculating global mean and then variance, we apply a very simple strategy. We can calculate the sum of elements \(\sum x_i\) and sum of square of the elements \(\sum x_i^2\) in each GPU, then apply all reduce operation to sum accross GPUs. Then calculate the global mean \(\mu=\frac{\sum x_i}{N}\) and global variance \(\sigma=\sqrt{\frac{\sum x_i^2}{N}-\mu^2+\epsilon}\)

• Backward Pass:

  • \(\frac{d_\ell}{d_{x_i}}=\frac{d_\ell}{d_{y_i}}\frac{\gamma}{\sigma}\) can be calculated locally in each GPU.
  • Calculate the gradient of sums \(\frac{d_\ell}{d_{\sum x_i}}\) and \(\frac{d_\ell}{d_{\sum x_i^2}}\). The gradients are handled by all reduce operation during the backward.

We discussed this Sync Once implementation in our recent paper Context Encoding for Semantic Segmentation.